The first unit I do with my 3rd grade math class every year leads to the conclusion, “Place-value would be so useful right now….” If I do it right, at least one kid ends up saying this. The goal of the unit is to get the kids to feel in their guts that place value is REALLY IMPORTANT to how we do arithmetic.
I learned this unit from another teacher who learned it from yet another teacher who… made it up? Learned it from someone else? Who knows. I think some of the best things are passed along, tinkered with, and adapted to the individual teacher’s teaching style.
The unit starts by taking the kids far into the past – all the way back to the time of the cavemen. The cavemen are about to do a remarkable thing: invent counting. Now, why would the cavemen do such a thing? The kids come up with very thoughtful answers to this question. “To keep track of things.” “To tell each other how much of something they have.” “To know if they’ve lost anything.” “To share.” These were all reasons that came up this year.
(We went on a tangent to discuss how you could compare amounts without counting. One kid came up with an awesome idea: drop both sets of things on the floor and have two people step on each thing at the same pace. The person who finishes first has less stuff. Especially since she’s now destroyed all of it.)
Once we know why the cavemen really need to invent counting (and fully appreciate how enormously difficult inventing such a thing could be), we learn how the cavemen counted.
I hold up one finger. “This is Na.” Note: it’s important not to say, “One is Na,” because the cavemen don’t have one. They have Na. And you don’t want the kids converting from our numbers to this system.
I hold up two fingers. “If you were a caveman, trying to make a really simple counting system, what would you call this?”
Kids suggest all sorts of things. But when a kid finally says, “Na Na,” they all nod. Clearly the cavemen wouldn’t make up a new word. Everybody can tell the difference between Na and Na Na, and it’s really easy to count when you only have Na or Na Na things. (We’ve just spent some time counting arrangements of dots quickly, so the kids already agree that one, two, and three things are easy to identify – but not higher.)
Three fingers is Na Na Na. But four fingers… now, that’s a lot of fingers. Na Na Na Na is quite a mouthful – and it’s getting hard to tell the numbers apart. Here is where the cavemen bring in a new word. Na Na Na Na is Ba.
We continue counting. Ba Na, Ba Na Na (giggles), Ba Na Na Na… now what? The kids think until… Ba Ba, of course!
Here is the Ba-Na-Na counting system, invented by cavemen so many years ago. The kids do some problems counting things in Ba-Na-Na and adding and subtracting – making sure to only use Ba-Na-Na, not normal numbers. Adding and subtracting is nice, we say, because it feels like adding and subtracting. To add, you just smush (and trade). To subtract, you remove (and trade).
But we eventually run into a problem. The BIG NUMBER problem.
It first comes up when someone wonders, “What’s Ba Ba Ba Ba?” It’s a natural question, and there’s always at least one kid ready with a good answer. “Za!” or “Ga!” or something like that. It doesn’t need to be a new word, but it makes writing numbers larger than Ba Ba Ba Na Na Na easier and is consistent with our logic from before. The kids are so excited by this discovery that it takes them a little longer to notice the larger problem.
“We’re going to run out of numbers.” This isn’t entirely true – you could just keep making up new words, and they don’t have to be two letters long and end in a. But, yes, we will run out of those words and – even worse – the system is going to get really, really complicated. How are we going to remember the order of the words? What started out as a very simple counting system gets very unwieldily when we try to write large numbers. The kids have lots of fun writing the largest possible number that uses “a” words with every letter of the alphabet – but they decide that the system is really no good for big numbers.
At this point, we bring normal numbers back in. What’s the difference between Ba Na Na and normal numbers, we wonder? I jog their brains by asking whether it matters what order you write the words in Ba Na Na. No…. Does it matter what order you write the numbers in our number system? Of course it does!
The big question is: What indicates size in Ba Na Na? What indicates size in our number system? In Ba Na Na, size is determined by the word – but in our number system, the word or symbol is much less important than where you write it. Because of place value, we only need ten words, but an infinite number of spots to write them – but because Ba Na Na relies only on words, it needs an infinite number of words. In which system is it easier to write big numbers?
Later in the year we’ll talk about which system is better for adding. Kids often like Ba Na Na better because adding is just accumulating more words, with a little trading. When you add, you actually get more words. When you add in our number system, you have to do a funny digit juggle that doesn’t “feel” like adding. We discuss how our number system trades adding that feels right for convenience of large numbers. Is this a good trade?
I like this unit for a variety of reasons, but mostly because it gives kids a way to truly understand the way place value works without relying on past good experiences with numbers. I also like it because it gives kids an opportunity to decide that they like place value – to choose our number system and commit to it. I’m proud of our number system when I’m done with this lesson. I fully understand its strengths and weaknesses and have decided that it’s worthy of my usage. That feels awesome.
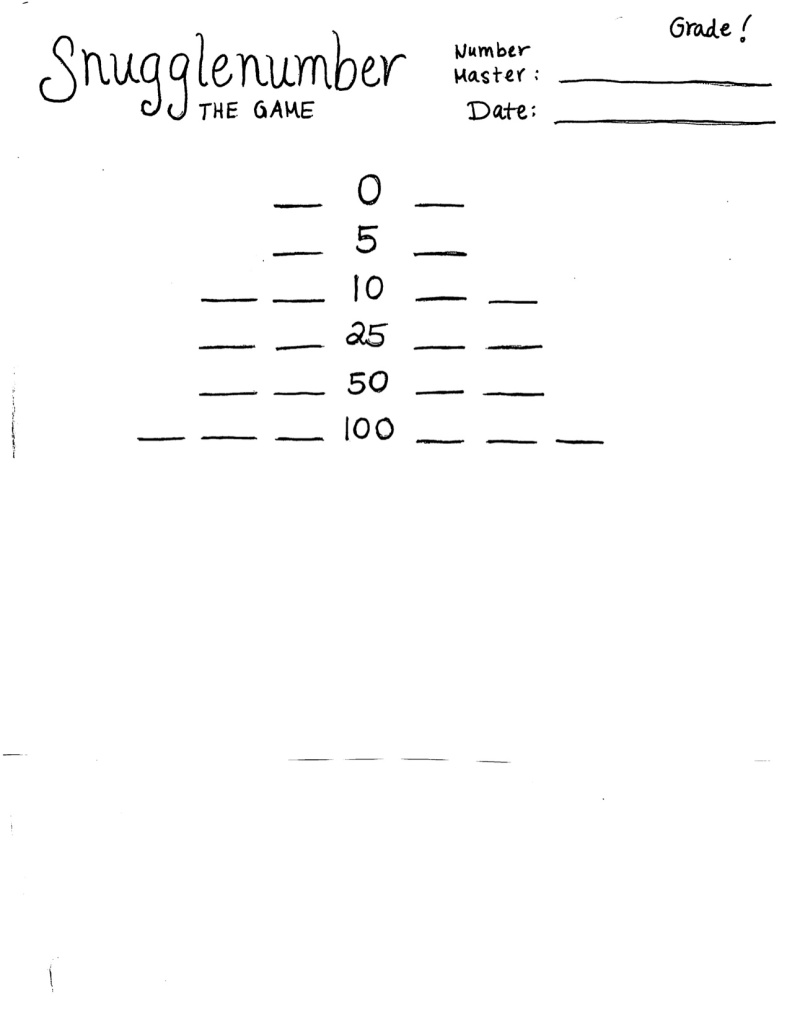And here’s how you play: It’s usually a two-player game, but I’ve played it with my whole class all at once – so it doesn’t really matter. Each player gets a board. You’ll notice that there are numbers down the middle. Those are the snugglenumbers. You’ll also notice that there are little dashes next to the numbers, to the right and left. That’s where you do your snuggling (lines on each side so that you can play two games).
Recipes for Pi 